Найдите площадь квадрата вписанного в окружность диаметром 2 (см, м, дм и тд).
В калькулятор мы вписываем значение R2 = D2 / 2 = 1 , то есть радиус описанной окружности.
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
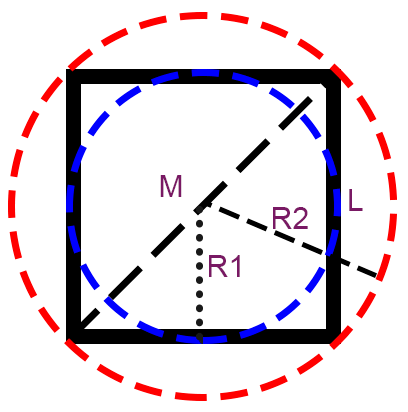
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Периметр квадрата (P)
Площадь квадрата (S)
Округление:
Знаков после запятой
2
* - обязательно заполнить
Радиус описанной окружности (R2) = 1
Диагональ, диаметр описанной окружности (M) =
Cторона, диаметр вписанной окружности (L) =
Радиус вписанной окружности (R1) =
Периметр (P) =
Площадь (S) =