Калькулятор отвечает на вопрос:

Найдите площадь квадрата с радиусом, равным 40.

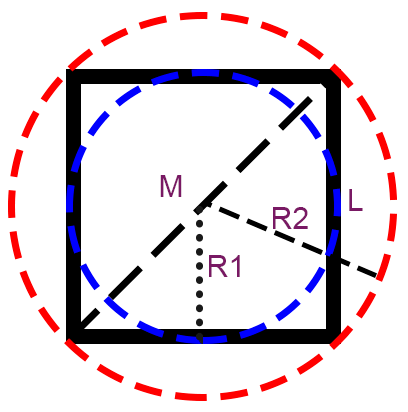
Мы взяли радиус описанной окружности, если нужен радиус вписанной окружности, то поменяйте его самостоятельно.

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Периметр квадрата (P)
Площадь квадрата (S)

Округление:

Знаков после запятой

* - обязательно заполнить

Радиус описанной окружности (R2) = 40

Диагональ, диаметр описанной окружности (M) = \(R2*2\) = \(40*2\) = 80

Cторона, диаметр вписанной окружности (L) = \(\sqrt{\frac{M^{2}}{2}}\) = \(\sqrt{\frac{80^{2}}{2}}\) = 56.57

Радиус вписанной окружности (R1) = \(\frac{L}{2}\) = \(\frac{56.57}{2}\) = 28.29

Периметр (P) = \(L*4\) = \(56.57*4\) = 226.28

Площадь (S) = \(L^{2}\) = \(56.57^{2}\) = 3200.16

Формулы

Площадь квадрата по радиусу вписанной окружности

Площадь квадрата равна радиусу вписанной окружности в квадрате умножить на 2.

S = R_{1}^{2}*2

Площадь квадрата по радиусу описанной окружности

Площадь квадрата равна половине квадрата радиуса описанной окружности, умноженного на 2.

S = \frac{(R_{2}*2)^{2}}{2}

Добавить комментарий